Research

Our research is directed at understanding and controlling the collective dynamics of quantum many-body systems far from equilibrium, which may ultimately pave the way to devise new technologies that rely on the quantum laws of nature. However, addressing them theoretically is a demanding task: For investigations based on microscopic model systems one has to devise strategies to deal with the curse of dimensionality inherent to the quantum many-body problem. Particularly challenging is the development of efficient and versatile computational methods that serve as crucial link between experimental observations and theoretical models. An alternative route is to use a quantum computer for the simulation, which – in turn – means to realize a highly controlled quantum-dynamical process.

Complex quantum dynamics

Neural quantum states

Reinforcement learning for quantum control

Showcase

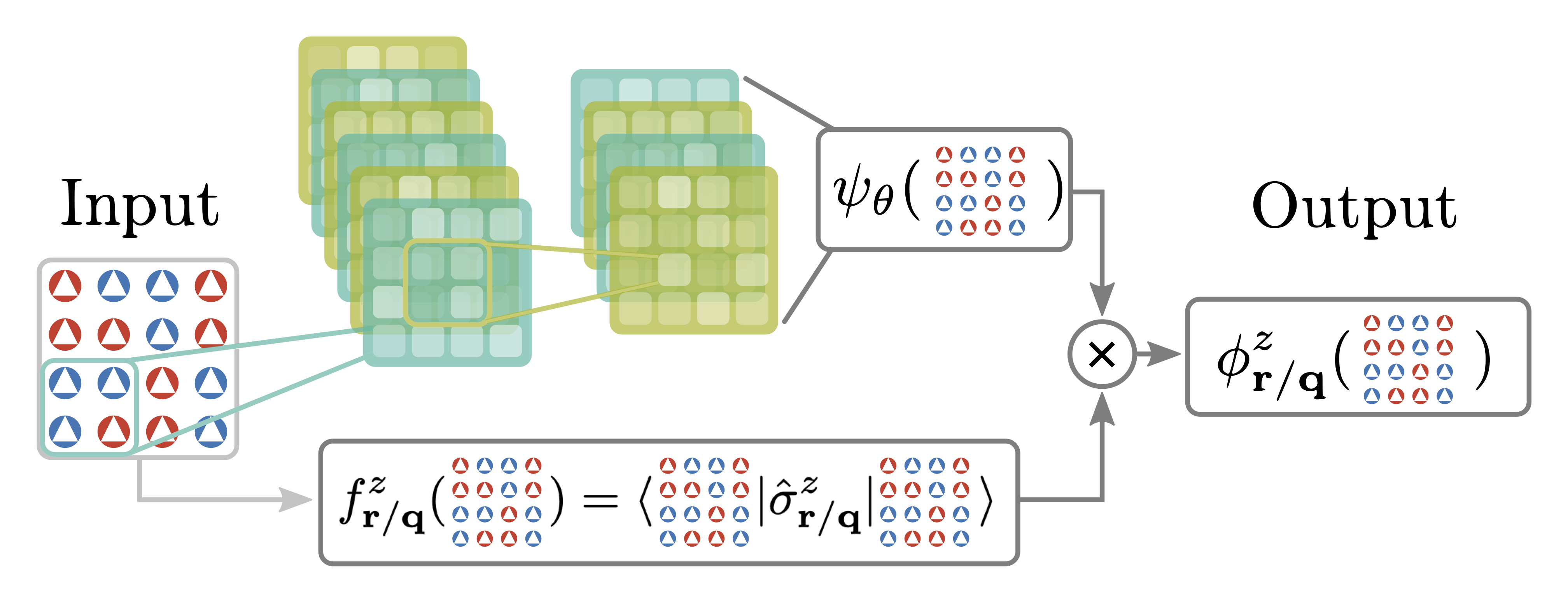
Highly resolved spectral functions of two-dimensional systems with neural quantum states

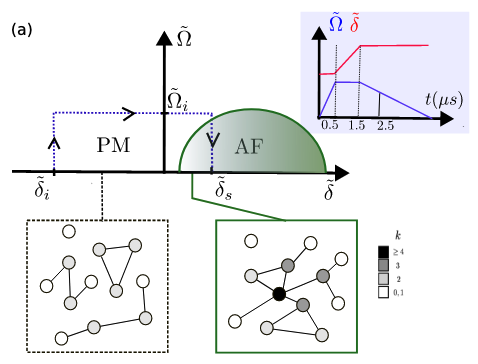
We developed a new approach to simulate spectral functions using neural quantum states, which for example accurately captures the gap closing at the phase transition of a two-dimensional quantum magnet despite the associated diverging time scale. Read more...

Phys. Rev. Lett. 131, 046501 (2023)

Wave function network description and Kolmogorov complexity of quantum many-body systems

Quantum Many-Body Jarzynski Equality and Dissipative Noise on a Digital Quantum Computer

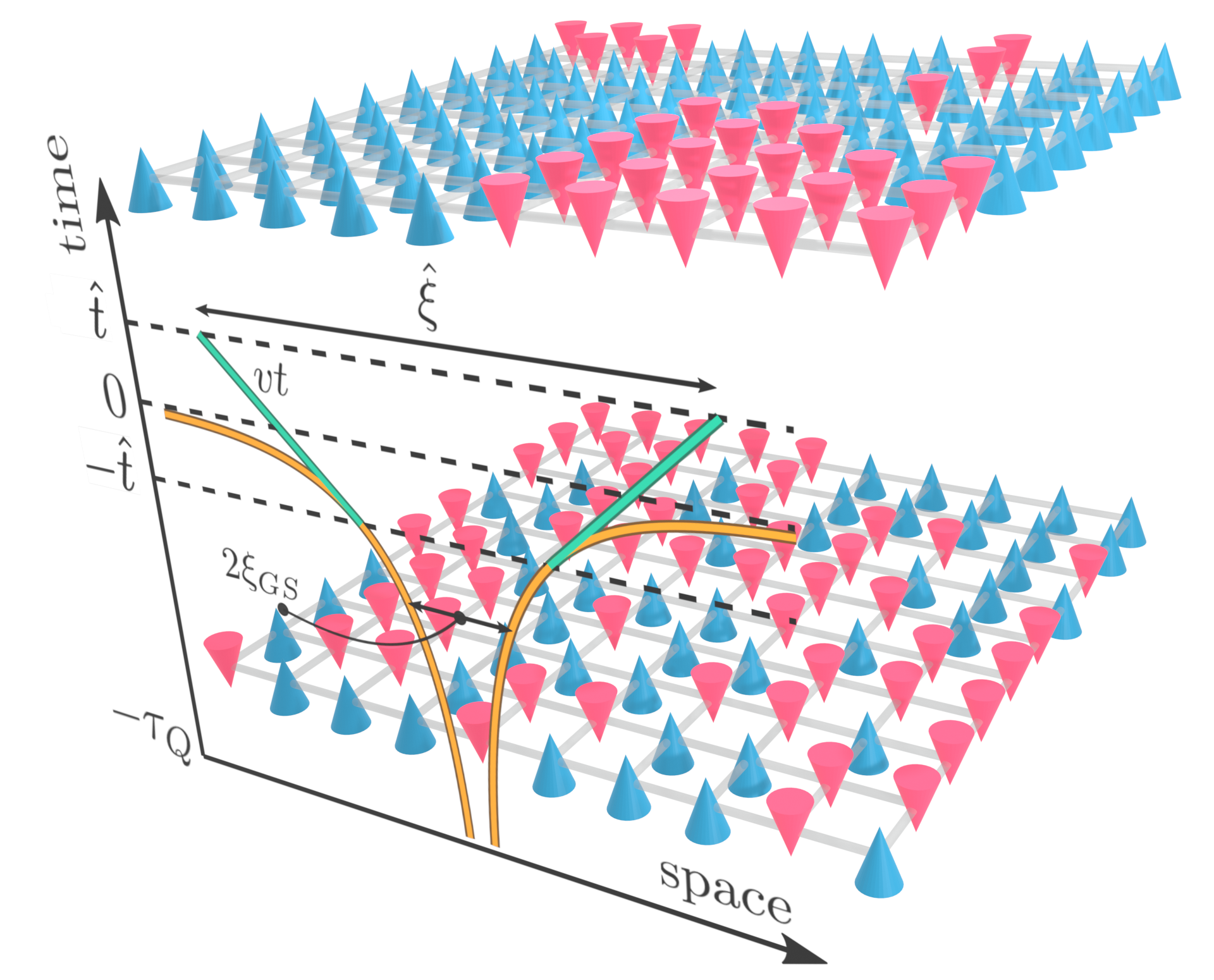
We explored fluctuations occuring in non-equilibrium processes implemented on a quantum processor, veryfying, for example, the Jarzynski equality in the regime of many interacting qubits. Read more...

Phys. Rev. X 13, 041023 (2023)

Quantum phase transition dynamics in the two-dimensional transverse-field Ising model

Based on simulations with tensor networks and neural quantum states we confirmed for the first time numerically the non-equilibrium scaling hypothesis of the Kibble-Zurek mechanism for a microscopic model system in two spatial dimensions. Read more...

Sci. Adv. 8, abl6850 (2022)

Time-dependent variational principle for open quantum systems with artificial neural networks

By generalizing the time-dependent variational principle to a purely probabilistic formulation of quantum mechanics we developed a new approach to simulate the time-evolution of open quantum many-body systems using, e.g., autoregressive neural networks. Read more...

Phys. Rev. Lett. 127, 230501 (2021)

Quantum many-body dynamics in two dimensions with artificial neural networks

By developing a number of methodological advancements we demonstrated for the first time that neural quantum states are competitive with state-of-the-art tensor network techniques when simulating complex quantum dynamics in two spatial dimensions. Read more...

Phys. Rev. Lett. 125, 100503 (2020)