Operator lanczos approach enabling neural quantum states as real-frequency impurity solvers

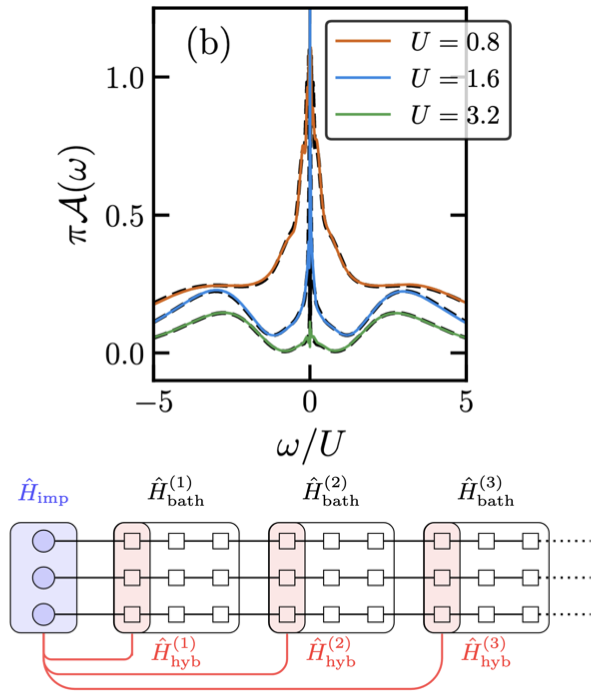
To understand the intricate exchange between electrons of different bands in strongly correlated materials, it is essential to treat multi-orbital models accurately. For this purpose, dynamical mean-field theory (DMFT) provides an established framework, whose scope crucially hinges on the availability of efficient quantum impurity solvers. Here we present a real-frequency impurity solver based on neural quantum states (NQS) combined with an operator-Lanczos construction. NQS are an asymptotically unbiased variational ground-state ansatz that employs neural networks to capture long-range correlations on complicated graph structures. We leverage this ability to solve multi-orbital impurity problems using a systematically improvable Segmented Commutator Operator-Lanczos (SCOL) construction. Our benchmarks on both the single-orbital Anderson model and the multi-orbital Hubbard-Kanamori impurity Hamiltonian reveal excellent ground-state precision and the capacity to accurately resolve zero temperature spectral functions and self-energies. These results open avenues for extending DMFT to more challenging problems.