Time evolution of the quantum Ising model in two dimensions using Tree Tensor Networks

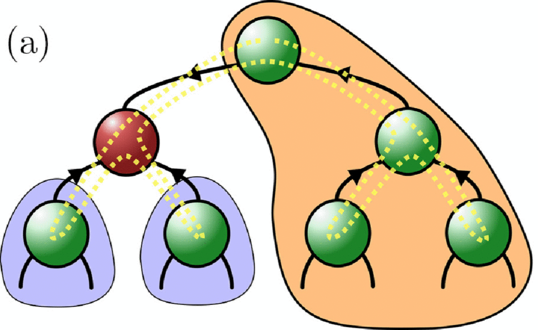
The numerical simulation of two-dimensional quantum many-body systems away from equilibrium constitutes a major challenge for all known computational methods. We investigate the utility of tree tensor network (TTN) states to solve the dynamics of the quantum Ising model in two dimensions. Within the perturbative regime of small transverse fields, TTNs faithfully reproduce analytically known, but nontrivial and physically interesting dynamics of magnetic domains, for lattices up to 16×16 sites. Limitations of the method related to the rapid growth of entanglement entropy are explored within more general, paradigmatic quench settings. We provide and discuss comprehensive benchmarks regarding the benefit of GPU acceleration and the impact of using local operator sums on the performance.