Reconstructing effective Hamiltonians from nonequilibrium thermal and prethermal steady states
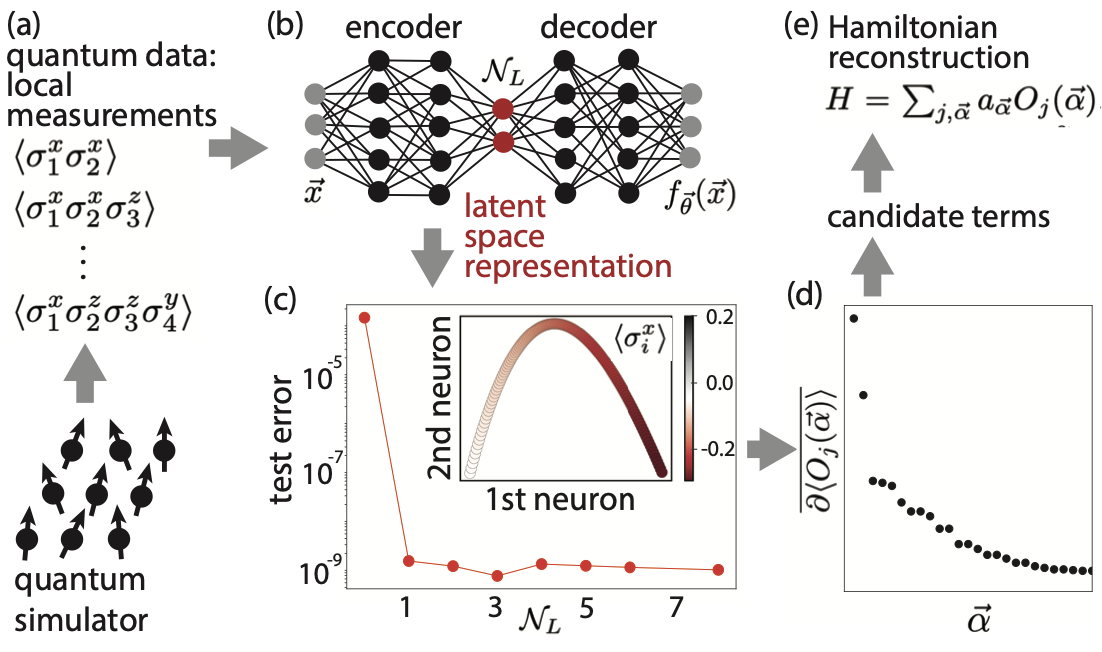
Reconstructing Hamiltonians from local measurements is key to enabling reliable quantum simulation: both validating the implemented model, and identifying any left-over terms with sufficient precision is a problem of increasing importance. Here we propose a deep-learning-assisted variational algorithm for Hamiltonian reconstruction by pre-processing a dataset that is diagnosed to contain thermal measurements of local operators. We demonstrate the efficient and precise reconstruction of local Hamiltonians, while long-range interacting Hamiltonians are reconstructed approximately. Away from equilibrium, for periodically and random multipolar driven systems, we reconstruct the effective Hamiltonian widely used for Floquet engineering of metastable steady states. Moreover, our approach allows us to reconstruct an effective quasilocal Hamiltonian even in the heating regime beyond the validity of the prethermal plateau, where perturbative expansions fail.