Highly resolved spectral functions of two-dimensional systems with neural quantum states

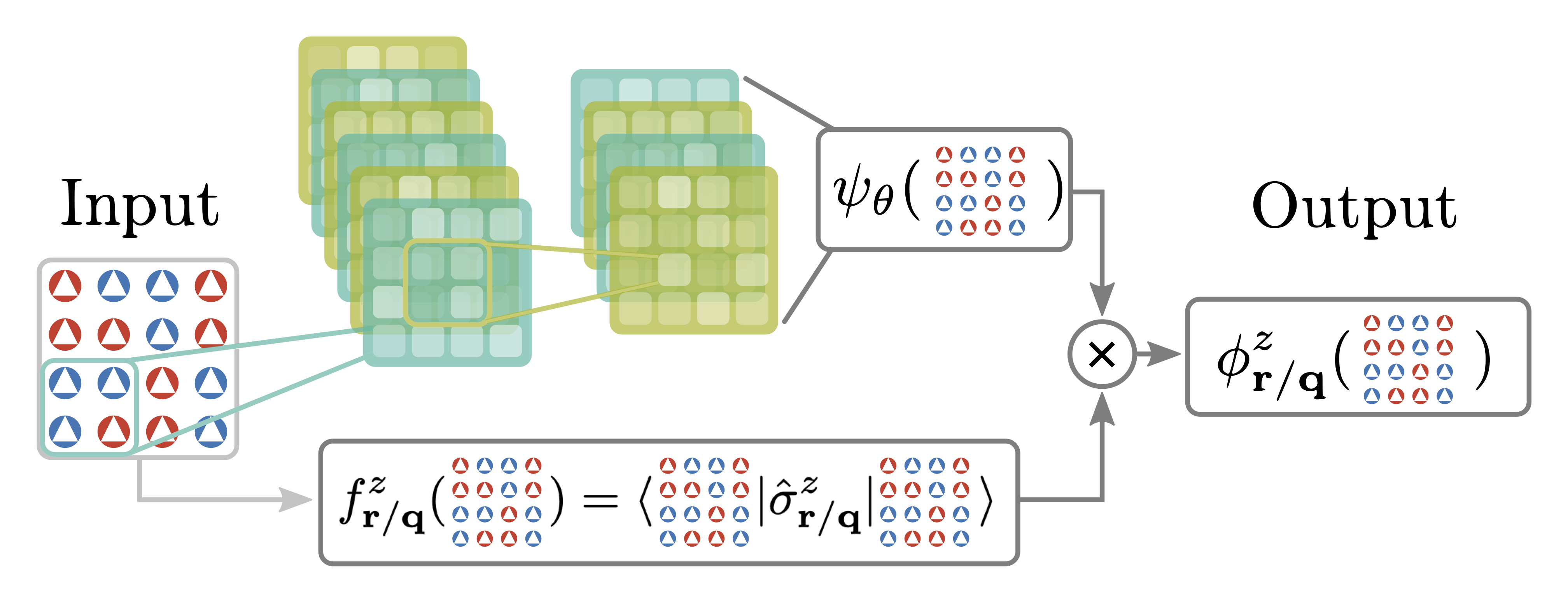
Spectral functions are central to link experimental probes to theoretical models in condensed matter physics. However, performing exact numerical calculations for interacting quantum matter has remained a key challenge especially beyond one spatial dimension. In this work, we develop a versatile and numerically exact approach using neural quantum states to obtain spectral properties based on simulations of the dynamics of excitations initially localized in real or momentum space. We apply this approach to compute the dynamical structure factor in the vicinity of phase transitions of different two-dimensional quantum Ising models, including one that describes the complex density wave orders of Rydberg atom arrays. When combined with deep network architectures we find that our method reliably describes dynamical structure factors of arrays with up to 24×24 spins, including the diverging time scales at critical points. Our approach is broadly applicable to interacting quantum lattice models in two dimensions and consequently opens up a route to compute spectral properties of correlated quantum matter in yet inaccessible regimes.