Wave function network description and Kolmogorov complexity of quantum many-body systems

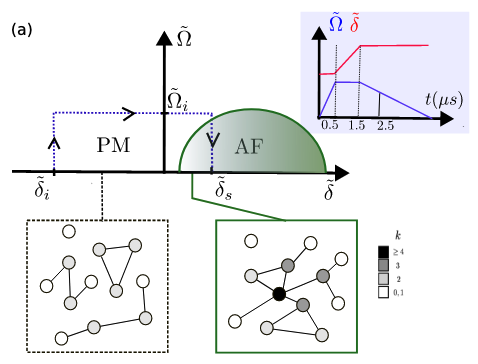
Programmable quantum devices are now able to probe wave functions at unprecedented levels. This is based on the ability to project the many-body state of atom and qubit arrays onto a measurement basis which produces snapshots of the system wave function. Extracting and processing information from such observations remains, however, an open quest. One often resorts to analyzing low-order correlation functions - i.e., discarding most of the available information content. Here, we introduce wave function networks - a mathematical framework to describe wave function snapshots based on network theory. For many-body systems, these networks can become scale free - a mathematical structure that has found tremendous success in a broad set of fields, ranging from biology to epidemics to internet science. We demonstrate the potential of applying these techniques to quantum science by introducing protocols to extract the Kolmogorov complexity corresponding to the output of a quantum simulator, and implementing tools for fully scalable cross-platform certification based on similarity tests between networks. We demonstrate the emergence of scale-free networks analyzing data from Rydberg quantum simulators manipulating up to 100 atoms. We illustrate how, upon crossing a phase transition, the system complexity decreases while correlation length increases - a direct signature of build up of universal behavior in data space. Comparing experiments with numerical simulations, we achieve cross-certification at the wave-function level up to timescales of 4 μ s with a confidence level of 90%, and determine experimental calibration intervals with unprecedented accuracy. Our framework is generically applicable to the output of quantum computers and simulators with in situ access to the system wave function, and requires probing accuracy and repetition rates accessible to most currently available platforms.