Optimizing Design Choices for Neural Quantum States

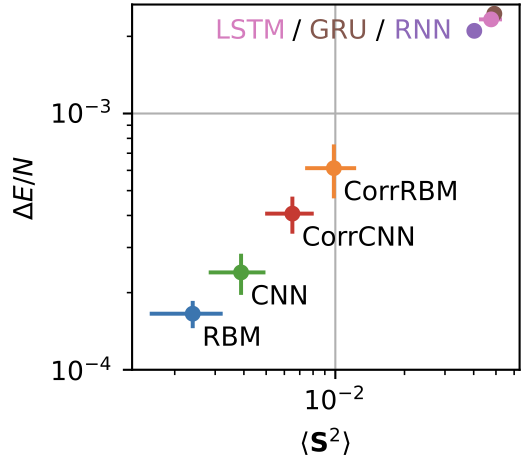
Neural quantum states are a new family of variational ansätze for quantum-many body wave functions with advantageous properties in the notoriously challenging case of two spatial dimensions. Since their introduction a wide variety of different network architectures has been employed to study paradigmatic models in quantum many-body physics with a particular focus on quantum spin models. Nonetheless, many questions remain about the effect that the choice of architecture has on the performance on a given task. In this work, we present a unified comparison of a selection of popular network architectures and symmetrization schemes employed for ground state searches of prototypical spin Hamiltonians, namely the two-dimensional transverse-field Ising model and the J1-J2 model. In the presence of a non-trivial sign structure of the ground states, we find that the details of symmetrization crucially influence the performance. We describe this effect in detail and discuss its consequences, especially for autoregressive models, as their direct sampling procedure is not compatible with the symmetrization procedure that we found to be optimal.